2020 GVSU Summer Mathematics REU Project:

Anti-Games on Steiner Triple Systems

Anti tic-tac-toe (also called toe-tac-tic, misere tic-tac-toe, or reverse tic-tac-toe) is played just like regular tic-tac-toe: Two players, called Xavier and Olivia, take turns selecting a point on a board. The only difference is that the first player to get 3 in a row loses.

If you're reading this, you should give this a try right now. Draw out a usual 3 by 3 tic-tac-toe board and play a few games.

It's possible to play tic-tac-toe style games on many different kinds of boards. For example, you could play tic-tac-toe in 3 by 3 by 3 cube. You might have seen torus tic-tac-toe, in which opposite sides of the board are connected. This lets winning lines wrap around the edges of the board. You can just as easily play anti torus tic-tac-toe. In general, you can play tic-tac-toe on any kind of board in which there are lines of 3-in-a-row, whatever those lines might be.

Here's an example of the usual tic-tac-toe board, where we've drawn in the lines instead of boxes. This time X lost anti tic-tac-toe:

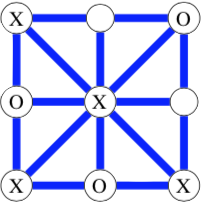
The goal of this project is to find winning strategies for anti tic-tac-toe when played on combinatorial objects called Steiner triple systems.

My anti tic-tac-toe project started in Summer 2013. Two of my students invented a new game played with SET cards. In this game, which we called "Anti-SET", players take turns picking up cards, trying to avoid a set. The first person to have a set in their hands loses.

These students found a winning strategy for this game.

You can visualize this strategy abstractly as in the image below, where each card is listed by X (Xavier) or O (Olivia) depending on which player took them. The subscripts indicate the order in which they were picked.

The proof of this strategy involved tools from linear algebra, modern (abstract) algebra, and combinatorics.

What does this have to do with anti tic-tac-toe? You can think of the sets in SET as the lines or three-in-a-rows of tic-tac-toe. When one player takes all three points in a row, or all three cards in a set, they've lost.

In 2014, we generalized this strategy to a larger class of geometric objects called ternary affine geometries, of which SET is one example. In these geometries, the points are the "cards" we play on, and lines are the "sets". It turns out that this game can be played on an infinite class of ternary affine geometries -- these are basically the same as tic-tac-toe, but on larger boards.

In 2017, my REU students studied anti tic-tac-toe to another kind of board. These boards are combinatorial objects called Steiner Triple Systems, or STSs.

STSs share many of the key geometric features of tic-tac-toe: The winning (or losing) lines have three points each, and every pair of points (boxes) are part of a unique line. However, STSs have more "wiggle room" than tic-tac-toe or affine geometries, and so games will be that much more interesting!

Here's an example of an anti-game played on a Steiner Triple System with 7 points, also called the Fano Plane:

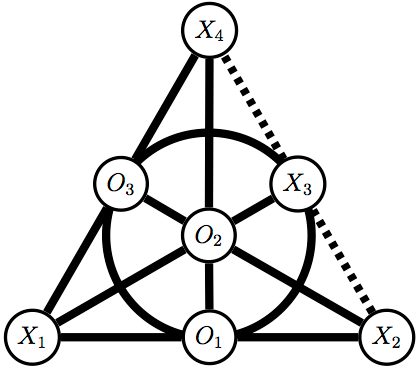
My 2017 REU students specifically examined Projective Binary STSs, which are a specific type of STS that has even nicer structure. They proved a winning strategy for the first player, Olivia.

Notice how in Anti-SET, Xavier (the 2nd player) wins. But in anti tic-tac-toe on Projective Binary STSs, Olivia (the 1st player) wins instead. This hints that interesting things are going on, and that the boards we play on make a big difference. Different boards can result in different winners -- what else might happen?

This summer research will involve generalizing anti tic-tac-toe to a broader category of Steiner Triple Systems. Our goal will be to see if we can extend the results from the previous anti tic-tac-toe papers to more types of STSs. In particular, we may study STSs made with the "doubling construction", which provides them with a structure similar to the Projective Binary STSs we studied in 2017.

The primary tools, techniques, and activities we will use will be:

• Playing sample games on a variety of concrete examples of STSs and analyzing the results. The goal is to determine if a winning strategy exists for one player, which player that is, and what the strategy is. This could be done using computer searches as well.
• Generalizing these results as broadly as we can. What properties of an STS determines who can win? What general statements can we make about these games?
• Looking for, reading, and understanding results about the structure of STSs that may help determine the winning strategy, as well as ways to allow a losing player to prolong the game.

I expect this to be more subtle than the story for previous games. We will begin by reviewing the techniques and arguments used by previous students, which I expect will be helpful as we study STSs.

Applicants should like discrete mathematics, aka Combinatorics. It will help to be comfortable with basic counting techniques (such as combinations and permutations) and combinatorial proofs (counting the same thing in two different ways, so as to find a formula).

Experience with Steiner Triple Systems and finite geometries is not necessary. We will learn key background material together as part of the project.

This project is not about game theory. I am not interested in studying Nash equilibria, pareto-optimal choices, etc. Instead, I am interested in analyzing combinatorial objects and learning how their properties affect this game.

You can find application information and instructions on the GVSU Summer Mathematics REU home page.